INASOFT 管理人のひとこと

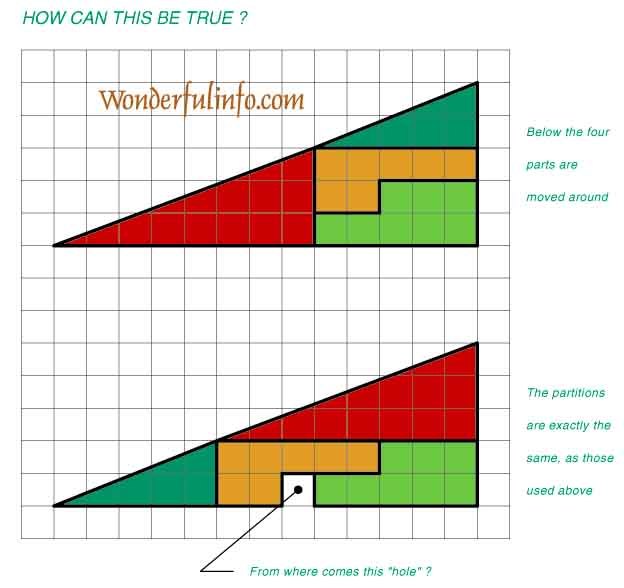
こんな図を頂いた。

んで、思い出したんです。数年前にも同じような図形を見せられて「ちょっとしたトリックだよ」と言われて。

後で真剣に考えてみようと思って、んで、すっかり忘れていたんです。思い出した！

早速解いてみることにします。

まず、この２つの図形、何が不思議かというと、上の図と下の図では、構成する各色のパーツはそれぞれ同じ物のはずなのに、その組み合わせ方により、あたかも面積が変わっているように見えている、というわけで。

上の図と比べて、下の図では１マス分足り無くなっちゃっていますから。

でも、パーツを見ても、違いは見られないし…、うーん。

分からない場合は、自分で作図してみましょう。斜めの線を引くときに、ちょっと違和感を感じるはず。アレ？と。

自分はここで気づきました。

この図形、わかりやすく周りにマス目が引いてあるけど、このマス目に対して正確にこの図形を作図することって難しい？

次に面積に着目。１マスが1cm×1cmのマス目であるということにして、合計となるはずの面積と、各パーツの面積を計算する。

赤いパーツは、8cm×3cm÷2＝12cm²

緑のパーツは、5cm×2cm÷2＝ 5cm²

黄色パーツは、7cm²

黄緑パーツは、8cm²

その合計は、32cm² となります。

で、上の図形の面積を素直に計算すると、13cm×5cm÷2＝32.5cm²

次に、下の図形の面積を素直に計算すると、上の面積より1cm²だけ小さいようなので、31.5cm²。

どちらも、0.5cm²ずつズレていますので、微妙なズレによるトリックが使われているだろうということが考えられます。

0.5cm²≒0.71cm×0.71cm なので、まぁまぁ微妙。

次に、赤い三角形と緑の三角形の、一番鋭い角の角度を見てみましょう。分度器をあてても良いですし、これらは直角三角形なのですから三角関数で計算しても構いません。

まぁここでは、文字で書き表したいので、三角関数で求めてみましょう。

緑の三角形は、底辺＝5cm、高さ＝2cm なので、arctan(2 / 5) ≒ 0.38ラジアン ≒ 21.8°

赤い三角形は、底辺＝8cm、高さ＝3cm なので、arctan(3 / 8) ≒ 0.36ラジアン ≒ 20.6°

ということで、緑の三角形と赤い三角形の２つは、鋭角の角度が違っております。

ここがトリックってことでしょう。

一番最初に作図をしたときにわかりますが、そもそも作図をしようとすると、マス目から微妙にずれてしまいます。それは、三角形の斜めの線の角度が違うから。

この差が微妙な隙間を作り出し、最初の２つの図形のようなトリックを生んでいるんでしょうね。

あぁ、久々に数学をやったなぁ。（三角関数の逆関数を駆使するところで。他は算数だ）